这是《机器学习中的数学基础》系列的第3篇。
- 矩阵的初步理解
在研究矩阵乘法之前,我们先来看看什么是矩阵。通俗地说,把多个向量并排放到一起,就叫做矩阵。比如下面这个2*2矩阵,就是由向量(2,1)和向量(5,3)组合到一起的:
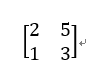
通常,我们所说的mxn的矩阵,是指矩阵有m行,n列。
- 矩阵的进一步理解
接下来,我们看矩阵和向量的乘法是什么样子的。先直接抛出定义的公式:
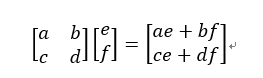
这个公式我们要好好研究下,把它研究透彻了,就能明白矩阵和向量的乘法中,矩阵到底扮演一个什么样的角色。
我们先来看结果,矩阵乘以向量,结果还是一个向量。不难看出,向量(ae+bf,ce+df)可以分解成两个向量的和。这两个向量分别是(ae,ce)和(bf,df),我们把公共的系数提出来,表示为:
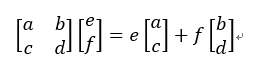
这是啥?这不就是向量(a,c)和向量(b,d)的线性组合吗?也就是说,矩阵乘以向量,就是以矩阵各列进行的线性组合,而这个线性组合的系数(权)就是向量的各个元素。通俗点说,矩阵乘以一个“旧”向量,把它变成了一个“新”向量。我们把这个变换,就叫做线性变换。也就是说,矩阵的作用就是一个线性变换。
- 矩阵的深层次理解
你以为这就结束了吗?并没有。下面我们将从基的角度再一次理解矩阵。
我们已经知道给定任意一个向量(e,f),它等价于(ei+fj),i和j是一组基。而这个“旧”向量(e,f),经过一个矩阵[a,b;c,d]的作用后,变成了“新”向量(eh+fk)。其中向量h=(a,c),向量k=(b,d)。对比前后两个新旧向量,你发现什么了吗?
你会发现,它们的系数是一样的,都是e和f。那这又说明什么呢?首先,可以看做又再一次验证了矩阵的作用确实是线性变换。其次,我们又需要一次思维跳跃。“旧”向量(ei+fj)我们把它看做由基i和j构成;那新向量(eh+fk)呢?我们也可以把它看成由新的基h和k构成。
重点来了,这次由某个矩阵“主导”的线性变换,只有基底发生了变化(从i、j到h、k)。我们把h和k放在一起,发现[h k]就是这个产生线性变换的矩阵啊。因此,我们看到的矩阵,竟然是一组基。当矩阵乘以向量时,得到的结果就是以矩阵的各列作为基,以旧向量元素为权(系数)而构造的一个新向量。
版权声明:本文来自用户投稿,不代表【闪电鸟】立场,本平台所发表的文章、图片属于原权利人所有,因客观原因,或会存在不当使用的情况,非恶意侵犯原权利人相关权益,敬请相关权利人谅解并与我们联系(邮箱:dandanxi6@qq.com)我们将及时处理,共同维护良好的网络创作环境。
