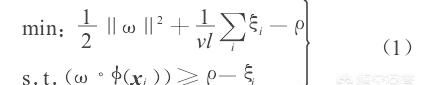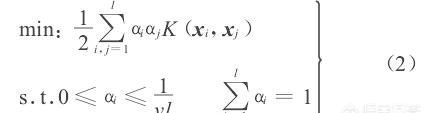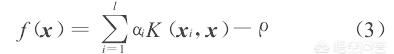一类支持向量机是在统计学习的理论基础上提出的一种无监督学习方法,其目的是将目标类样本与其他样本进行有效区分,具有无需先验知识和结构风险最小化等优点,因此被广泛应用于异常检测和故障诊断中。
一类支持向量机的基本原理如下:假设有源于同一分布的n维向量样本x1,x2,… ,xl∈ Rn,通过非线性函数将样本映射到高维的特征空间F中,在F中寻找一个体积小而包含样本点尽可能多的区域,使其与非本类样本以最大间隔分开.以二次型方程来表示该优化问题
式中:ω为超平面法向量;ρ为边界系数;ξi≥ 0为松弛因子;l为样本点数;0< v≤ 1为折衷系数,它决定分布区域的体积与包含样本点多少的折衷.该方程从空间几何的角度来看,是将样本投影到一个超球体中,寻找一个与ω正交、距离球心ρ/‖ω‖的超平面,使大多数样本处于被超平面分割并远离超球中心的区域,为保证该区域的结构紧凑,少数样本被排除在分布区域之外,与边界的距离为ξi。
构造拉格朗日函数求解式(1),化简后得到
式中:αi为拉格朗日系数;K为核函数;K(xi,xj)为(xi)和 (xj)的内积运算,并记做Ki,j.式(2)是典型的二次规划问题,求解得到的αi多数等于0,只有少部分αi大于0,将其对应的样本xi称为支持向量.
定义决策函数
当f(x)> 0时,x位于样本的分布区域之内,f(x)= 0时,x位于分布区域边界上,f(x)< 0时,x
位于样本分布区域之外.由式(3)可知,αi= 0的样本在计算中将被忽略,因此全体目标样本在特征空间中的分布仅取决于支持向量。
版权声明：本文来自用户投稿，不代表【闪电鸟】立场，本平台所发表的文章、图片属于原权利人所有，因客观原因，或会存在不当使用的情况，非恶意侵犯原权利人相关权益，敬请相关权利人谅解并与我们联系（邮箱：dandanxi6@qq.com）我们将及时处理，共同维护良好的网络创作环境。