神秘的莫比乌斯环,莫比乌斯环解密

一条边、一个面的物体长啥样

文章开始前，我先来问大家几个问题：

1、一个长方形纸条，有几条边、几个面？

这个很简单，你肯定知道：四条边，两个面。

2、如何把一张长方形纸条变成只有两条边、两个面呢？

这个其实也不难，把长方形纸条首尾相接，粘成一个圆柱形。

3、怎么把长方形纸条变成一条边、一个面呢？

这是一个难题，带着这个疑问，咱们先来看个小故事。

这个问题曾经困扰了无数科学家，却始终没能解决。德国数学家莫比乌斯便是其中一位，他对这个问题长时间专心思索、试验，毫无结果。

1858年的一天，他去野外散步，来到一片玉米地。叶子弯曲着耸拉下来，有许多扭成半圆形的，他随便撕下了一片，顺着叶子自然扭的方向对接成一个圆圈儿，他惊喜地发现，这“绿色的圆圈儿”就是他梦寐以求的答案。

他高兴地回到到办公室，裁出纸条，把纸的一端扭转180°，再将一端的正面和背面粘在一起，这样就做成了特殊的纸圈儿——莫比乌斯环。

接着，莫比乌斯捉了一只小甲虫，放在上面让它爬，小甲虫不翻越任何边界就爬遍了圆圈儿的所有部分。之后这种神奇的圈被命名为莫比乌斯环，它有一个最令人著迷的性质：它只有一条边和一个面。

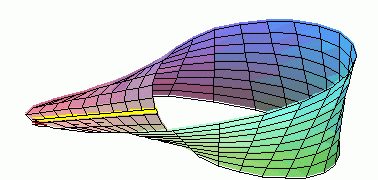
莫比乌斯环的玩法

这个神奇的环，除了只有一条边和一个面之外，还有很多好玩的方式，一起来了解下吧。

若是在莫比乌斯环的中间画上一条线，然后用剪刀沿着这条线剪开这个莫比乌斯环，将会得到什么呢？

如果沿着莫比乌斯环中间剪开，和一般的纸带（会分成断开的两条环）不一样，而会形成一个比原来的莫比乌斯环周长大一倍、把纸带的端头扭转了四次再粘合一起的环。

若是在莫比乌斯环的三等分处画一条线，然后用剪刀沿着这条线剪开这个莫比乌斯环，将会得到什么呢？

如果沿着莫比乌斯环三等分处剪开，剪刀绕两个圈竟又回到原出发点，这时会形成两个纸环，其中一条和原来的周长一样长，另一条则比原来的莫比乌斯环周长大一倍，而且两条是套在一起的。

若是在莫比乌斯环的四等分处画一条线，然后用剪刀沿着这条线剪开这个莫比乌斯环，又会得到什么呢？

如果沿着莫比乌斯环四等分处剪开，这时会形成两条比原来的莫比乌斯环周长都大一倍纸环，而且两条是套在一起的。

上面这几个都是一个环剪开，下面，咱们再来看看两个环剪开会是什么样！

首先我们先将两个正常的的纸环粘在一起剪开，猜猜会是什么形状呢？

是一个空心的正方形。接下来，我们试着将两个莫比乌斯环（把纸的一端扭转180°）粘在一起剪开。

啊哈，这次是两个套在一起的心形！我们再试试把纸的两端都旋转180°，把纸环沿两条三等分线剪开，猜猜是什么样呢？

是三个套在一起的纸环。

有没有觉得不可思议呢？关于莫比乌斯环，你还能想到哪些好玩的剪法呢？

生活中的莫比乌斯环

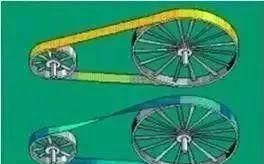
1、莫比乌斯环传送带

1979年，美国著名轮胎公司百路驰创造性地把传送带制成莫比乌斯环形状，这样一来，整条传送带环面各处均匀地承受磨损，避免了普通传送带单面受损的情况，使得其寿命延长了整整一倍。

2、莫比乌斯环标志

莫比乌斯圈循环往复的几何特征，蕴含着永恒、无限的意义，因此常被用于各类标志设计。微处理器厂商Power Architecture的商标就是一条莫比乌斯环，Power Architecture技术是一个主流平台，被广泛应用于包括汽车控制、远程通讯、无线和有线基础架构、企业网络、服务器和数字家庭。

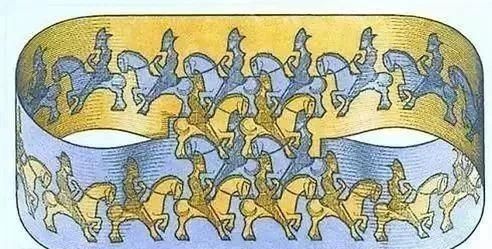
3、莫比乌斯艺术

莫比乌斯环艺术有很多，但荷兰图形艺术家M.C.埃舍尔的《莫比乌斯带》系列最能表现莫比乌斯环的生动形象，同时也是最具震撼力的作品。