下面让我们来思考这样一个问题。
比方说有一个物体,我们现在用这个U(x) 代表此物体随着其位移变化的势能。比方说这样一个曲线:
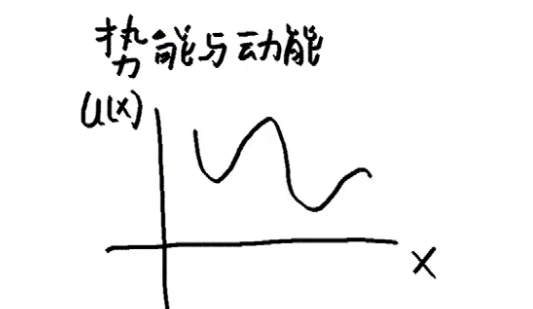
那么我们可以根据这个物体的位移,以及根据这个曲线找出与位移对应状态的物体的势能是多少。

那么我假设这个系统是一个能量守恒的系统 ,也就是说物体的势能加上此物体的这个其他的能量是一个守恒值。
那么现在我们把这个系统考虑得简单一点,就只考虑势能和动能。也就是说在这个守恒的系统中,除了物体的这个势能(potential energy)以外,就是物体的动能(kinetic energy),那么我们用这个动能的表达式:(1/2)*m*v^2来表示这个物体的动能。用U(x) 表达此物体的势能(potential energy),动能(KE)与势能(PE)的和为系统的总能量,为一个恒定值E。
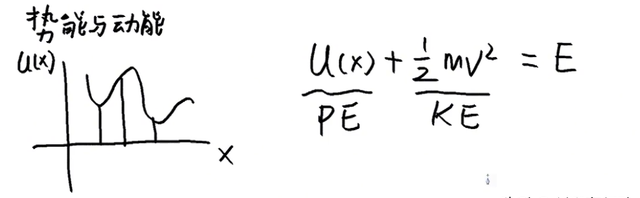
那我们下面再来分析一个问题。
如果我们现在对势能和动能的和等于恒定值的方程来求对于时间t的导数,我们会得到什么呢?
因为E是常数 ,所以对t求导就直接变成零了!
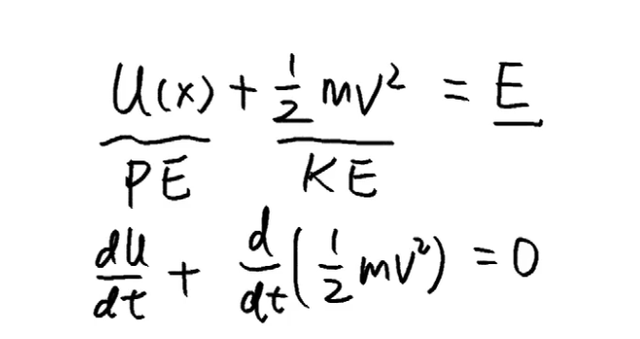
然后我们看一下动能这部分项。
为求动能对于时间的导数,实际上我们是要应用一个叫做复合函数求导法则的技巧,我们把这法则写出来:
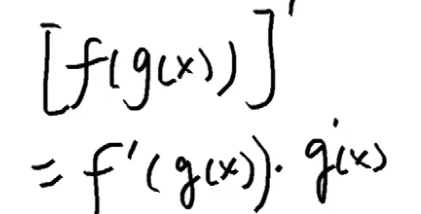
现在我们用位移的方式去表达速度,有:
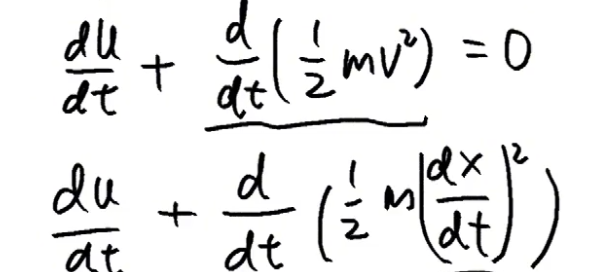
好,我们来看一看这样会产生一个什么样的效果?
根据这个复合函数求导法则,我们可以得到如下结论:
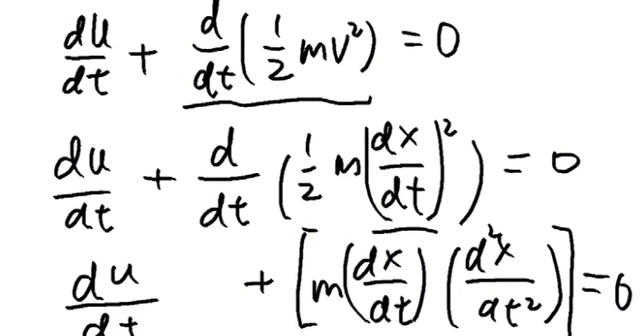
这是符合函数求导法则的应用!
那么我们现在来观察一下这个式子,我们把最后一行的式子保留下来,有:
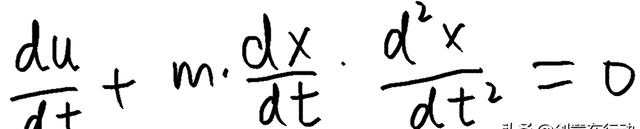
我们现在可以对上式进行变形以及进一步整理式子我们得到:
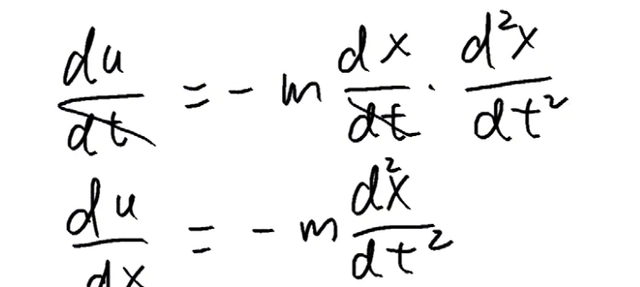
我们观察上式最后一行的右边的项,可以看出这是用位移的方式来表达的物体的受力的负值,即:
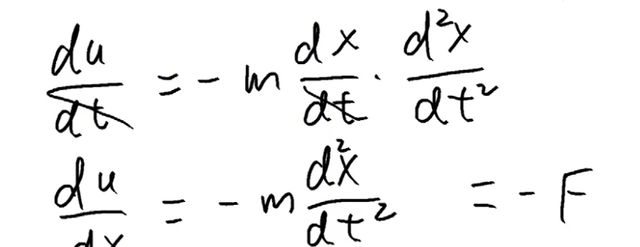
到这里我们得到了物体势能对于位移的导数与物体受力的关系!
我们可以写成如下的形式:
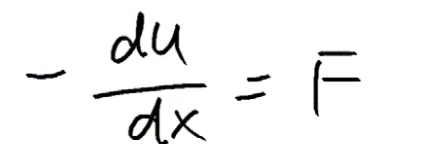
在这个系统中势能和动能相互转化,但是总能量是不变的!
根据物体的势能随物体位移的变化关系曲线我们可以分析出物体的受力情况,这是广义的情况,如果举例子,比如在地球的真空环境中将物体上抛 ,地球的的引力对物体作用实现重力势能与物体动能的转换,再比如一端固定的弹簧拉动砝码产生的简谐运动中,弹簧对物体的拉力实现了弹性势能与砝码动能的转换!
那么如果我们给出任意的 U(x)曲线,那么当物体处于切线斜率为零的点的状态时物体的受力如何呢,由上述方程可知此状态下的物体不受力,举一个例子:当弹簧拉动砝码做简谐运动时当弹簧处于松弛状态时砝码不受力!当然 对于地球上真空中物体上抛运动而言,由于重力作用一直存在,所以U(x)曲线不会出现切线斜率为零的点,这你想到了吗?
版权声明:本文来自用户投稿,不代表【闪电鸟】立场,本平台所发表的文章、图片属于原权利人所有,因客观原因,或会存在不当使用的情况,非恶意侵犯原权利人相关权益,敬请相关权利人谅解并与我们联系(邮箱:dandanxi6@qq.com)我们将及时处理,共同维护良好的网络创作环境。
